At the heart of any vector database are the distance functions that determine how close two vectors are. These distance functions are executed many times, both during indexing and searching. When merging segments or navigating the graph for nearest neighbors, much of the execution time is spent comparing vectors for similarity. Micro optimizing these distance functions is time well spent, we're already benefiting from similar previous optimizations, e.g. see SIMD, FMA.
With the recent support for scalar quantization in both Lucene and Elasticsearch, we're now more than ever leaning on the byte variants of these distance functions. We know from previous experience that there's still the potential for significant performance improvements in these variants.
Current state of play: The Panama Vector API
When we leveraged the Panama Vector API to accelerate the distance functions in Lucene, much of the focus was on the float (32-bit) variants. We were quite happy with the performance improvements we managed to achieve for these. However, the improvements for the byte (8-bit) variants was a little disappointing - and believe me, we tried! The fundamental problem with the byte variants is that they do not take full advantage of the most optimal SIMD instructions available on the CPU.
When doing arithmetic operations in Java, the narrowest type is int (32-bit). The JVM automatically sign-extends byte values to values of type int. Consider this simple scalar dot product implementation:
int dotProduct(byte[] a, byte[] b) {
int res = 0;
for (int i = 0; i < a.length; i++) {
res += a[i] * b[i];
}
return res;
}The multiplication of elements from a and b is performed as if a and b are of type int, whose value is the byte value loaded from the appropriate array index sign-extended to int.
Our SIMD-ized implementation must be equivalent, so we need to be careful to ensure that overflows when multiplying large byte values are not lost. We do this by explicitly widening the loaded byte values to short (16-bit), since we know that all signed byte values when multiplied will fit without loss into signed short. We then need a further widen to int (32-bit) when accumulating.
Here's an excerpt from the inner loop body of Lucene's 128-bit dot product code:
ByteVector va8 = ByteVector.fromArray(ByteVector.SPECIES_64, a, i);
ByteVector vb8 = ByteVector.fromArray(ByteVector.SPECIES_64, b, i);
// process first "half" only: 16-bit multiply
Vector<Short> va16 = va8.convert(B2S, 0); // B2S Byte2Short
Vector<Short> vb16 = vb8.convert(B2S, 0);
Vector<Short> prod16 = va16.mul(vb16);
// 32-bit add - S2I Short2Int
acc = acc.add(prod16.convertShape(S2I, IntVector.SPECIES_128, 0));Visualizing this we can see that we're only processing 4 elements at a time. e.g.
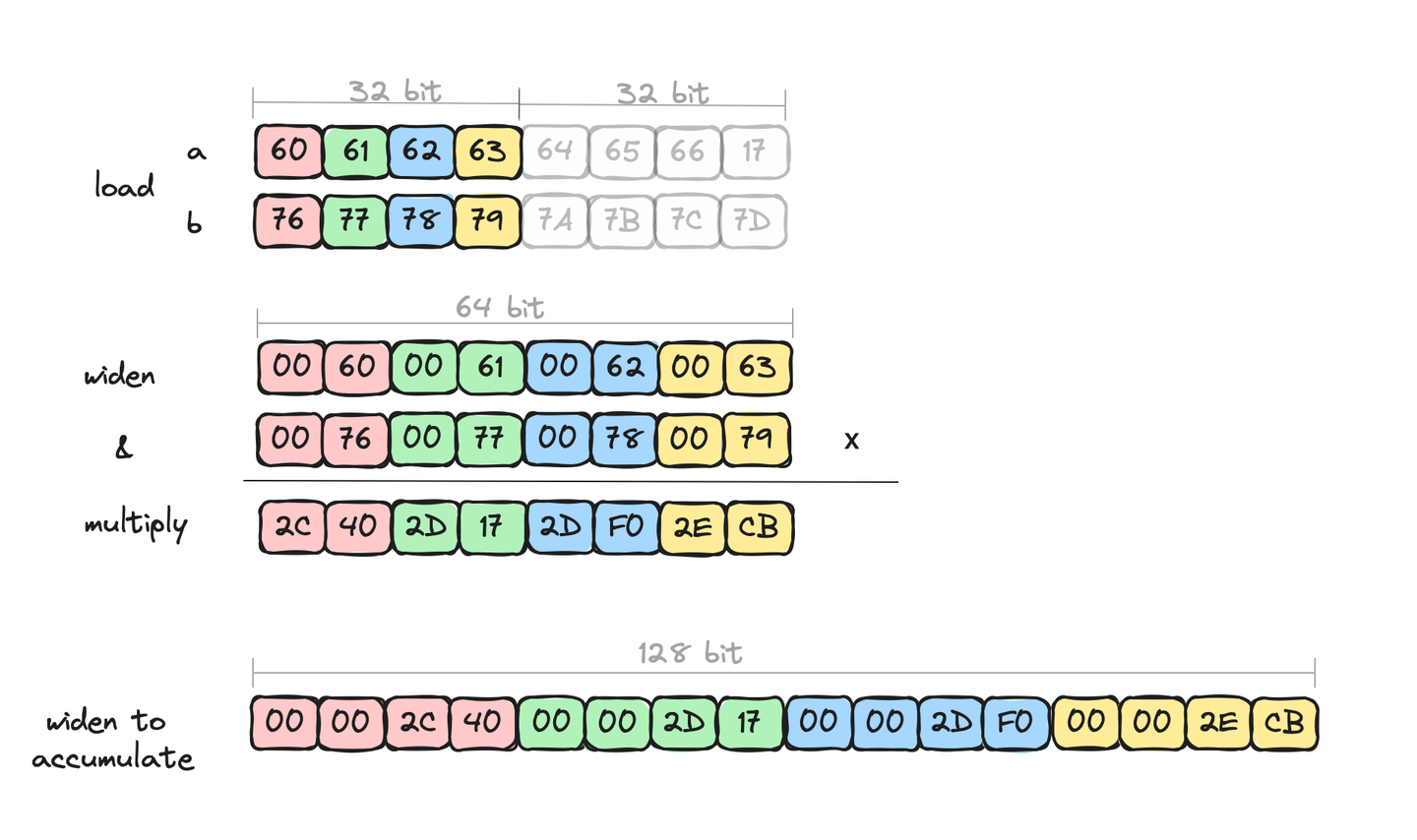
This is all fine, even with these explicit widening conversations, we get some nice speed up through the extra data parallelism of the arithmetic operations, just not as much as we know is possible. The reason we know that there is potential left is that each widening halves the number of lanes, which effectively halves the number of arithmetic operations. The explicit widening conversations are not being optimized by the JVM's C2 JIT compiler. Additionally, we're only accessing the lower half of the data - accessing anything other than the lower half just does not result in good machine code. This is where we're leaving potential performance "on the table".
For now, this is as good as we can do in Java. Longer term, the Panama Vector API and/or C2 JIT compiler should provide better support for such operations, but for now, at least, this is as good as we can do. Or is it?
Introducing the Foreign Function & Memory (FFM) API
OpenJDK's project Panama has several different strands, we've already seen the Panama Vector API in action, but the flagship of the project is the Foreign Function & Memory API (FFM). The FFM API offers a low overhead for interacting with code and memory outside the Java runtime. The JVM is an amazing piece of engineering, abstracting away much of the differences between architectures and platforms, but sometimes it's not always possible for it to make the best tradeoffs, which is understandable. FFM can rescue us when the JVM cannot easily do so, by allowing the programmer to take things into her own hands if she doesn't like the tradeoff that's been made. This is one such area, where the tradeoff of the Panama Vector API is not the right one for byte sized vectors.
FFM usage example
We're already leveraging the foreign memory support in Lucene to mediate safer access to mapped off-heap index data. Why not use the foreign invocation support to call already optimized distance computation functions? Since our distance computation functions are tiny, and for some set of deployments and architectures for which we already know the optimal set of CPU instructions, why not just write the small block of native code that we want. Then invoke it through the foreign invocation API.
Going foreign
Elastic Cloud has a profile that is optimized for vector search. This profile targets the ARM architecture, so let's take a look at how we might optimize for this.
Let's write our distance function, say dot product, in C with some ARM Neon intrinsics. Again, we'll focus on the inner body of the loop. Here's what that looks like:
int32x4_t acc1, acc2 // = vdupq_n_s32(0);
...
// Read into 16 x 8 bit vectors.
int8x16_t va8 = vld1q_s8((const void*)(a + i));
int8x16_t vb8 = vld1q_s8((const void*)(b + i));
int16x8_t va16 = vmull_s8(vget_low_s8(va8), vget_low_s8(vb8));
int16x8_t vb16 = vmull_s8(vget_high_s8(va8), vget_high_s8(vb8));
// Accumulate 4 x 32 bit vectors (adding adjacent 16 bit lanes).
acc1 = vpadalq_s16(acc1, va16);
acc2 = vpadalq_s16(acc2, vb16);We load 16 8-bit values from our a and b vectors into va8 and vb8, respectively. We then multiply the lower half and store the result in va16 - this result holds 8 16-bit values and the operation implicitly handles the widening. Similar with the higher half. Finally, since we operated on the full original 16 values, it's faster to use to two accumulators to store the results. The vpadalq_s16 add and accumulate intrinsic knows how to widen implicitly as it accumulates into 4 32-bit values. In summary, we've operated on all 16 byte values per loop iteration. Nice!
The disassembly for this is very clean and mirrors the above instrinsics.
ldr q2, [x1, x8] # loads first vector data into 128-bit q2
ldr q3, [x2, x8] # loads second vector data into 128-bit q3
smull.8h v4, v2, v3 # multiplies low half, result in v4
smull2.8h v2, v2, v3 # multiplies high half, result in v2
sadalp.4s v0, v4 # accumulates into v0
sadalp.4s v1, v2 # accumulates into v1Neon SIMD on ARM has arithmetic instructions that offer the semantics we want without having to do the extra explicit widening. The C instrinsics expose these instructions for use in a way that we can leverage. The operations on registers densely packed with values is much cleaner than what we can do with the Panama Vector API.
Back in Java-land
The last piece of the puzzle is a small "shim" layer in Java that uses the FFM API to link to our foreign code. Our vector data is off-heap, we map it with a MemorySegment, and determine offsets and memory addresses based on the vector dimensions.
The dot product method looks like this:
static int dot8s(MemorySegment a, MemorySegment b, int dims) {
var mh$ = dot8s$MH();
try {
return (int)mh$.invokeExact(a, b, dims);
} catch (Throwable ex$) {
...
}
}We have a little more work to do here since this is now platform-specific Java code, so we only execute it on aarch64 platforms, falling back to an alternative implementation on other platforms.
So is it actually faster than the Panama Vector code?
Performance improvements with FFM API
Micro benchmarks of the above dot product for signed byte values show a performance improvement of approximately 6 times, than that of the Panama Vector code. And this includes the overhead of the foreign call. The primary reason for the speedup is that we're able to pack the full 128-bit register with values and operate on all of them without explicitly moving or widening the data.
Macro benchmarks, SO_Dense_Vector with scalar quantization enabled, shows significant improvements in merge times, approximately 3 times faster - the experiment only plugged in the optimized dot product for segment merges. We expect search benchmarks to show improvement too.
Summary
Recent advancements in Java, namely the FFM API, allows to interoperate with native code in a much more performant and straightforward way than was previously possible. Significant performance benefits can be had by providing micro-optimized platform-specific vector distance functions that are called through FFM.
We're looking forward to a future version of Elasticsearch where scalar quantized vectors can take advantage of this performance improvement. And of course, we're giving a lot of thought to how this relates to Lucene and even the Panama Vector API, to determine how these can be improved too.
Ready to try this out on your own? Start a free trial.
Elasticsearch and Lucene offer strong vector database and search capabilities. Dive into our sample notebooks to learn more.
Related content

September 3, 2025
Vector search filtering: Keep it relevant
Performing vector search to find the most similar results to a query is not enough. Filtering is often needed to narrow down search results. This article explains how filtering works for vector search in Elasticsearch and Apache Lucene.

April 7, 2025
Speeding up merging of HNSW graphs
Explore the work we’ve been doing to reduce the overhead of building multiple HNSW graphs, particularly reducing the cost of merging graphs.

April 7, 2025
Speeding up HNSW graph merge
We describe a new strategy we developed that reduces HNSW merge time by up to 70% whilst maintaining similar graph quality

February 27, 2025
Filtered HNSW search, fast mode
Explore the improvements we have made for HNSW vector search in Apache Lucene through our ACORN-1 algorithm implementation.
February 7, 2025
Concurrency bugs in Lucene: How to fix optimistic concurrency failures
Thanks to Fray, a deterministic concurrency testing framework from CMU’s PASTA Lab, we tracked down a tricky Lucene bug and squashed it