As we continue on our mission to make Elasticsearch and Apache Lucene the best place to store and search your vector data, we introduced a new approach in BBQ (Better Binary Quantization). BBQ is a huge step forward, bringing significant (32x) efficiencies by compressing the stored vectors, while maintaining high ranking quality and at the same time offering Smokin' Fast performance. You can read about how BBQ quantizes float32 to single bit vectors for storage, outperforms traditional approaches like Product Quantization in indexing speed (20-30x less quantization time) and query speed (2-5x faster queries), see the awesome accuracy and recall BBQ achieves for various datasets, in the BBQ blog.
Since high-level performance is already covered in the BBQ blog, here we'll go a bit deeper to get a better understanding of how BBQ achieves such great performance. In particular, we'll look at how vector comparisons are optimized by hardware accelerated SIMD (Single Instruction Multiple Data) instructions. These SIMD instructions perform data-level parallelism so that one instruction operates on multiple vector components at a time. We'll see how Elasticsearch and Lucene target specific low-level SIMD instructions, like the AVX's VPOPCNTQ on x64 and NEON's vector instructions on ARM, to speed up vector comparisons.
Why do we care so much about comparing vectors?
Vector comparisons dominate the execution time within a vector database and are commonly the single most costly factor. We see this in profile traces, whether it be with float32, int8, int4, or other levels of quantization. This is not surprising, since a vector database has to compare vectors a lot! Whether it be during indexing, e.g. building the HNSW graph, or during search as the graph or partition is navigated to find the nearest neighbours. Low-level performance improvements in vector comparisons can be really impactful on overall high-level performance.
Elasticsearch and Lucene support a number of vector similarity metrics, like dot product, cosine, and Euclidean, however we'll focus on just dot product, since the others can be derived from that. Even though we have the ability in Elasticsearch to write custom native vector comparators, our preference is to stay in Java-land whenever possible so that Lucene can more easily get the benefits too.
Comparing query and stored vectors
For our distance comparison function to be fast, we need to simplify what it's doing as much as possible so it translates to a set of SIMD instructions that execute efficiently on the CPU. Since we've quantized the vectors to integer values we can load more of their components into a single register and also avoid the more costly floating-point arithmetic - this is a good start, but we need more.
BBQ does asymmetric quantization; the query vector is quantized to int4, while the stored vectors are even more highly compressed to just single bit values. Since a dot product is the sum of the product of the component values, we can immediately see that the only query component values that can contribute positively to the result are the values where the stored vector is 1.
A further observation is that if we translate the query vector in a way where the respective positional bits (1, 2, 3, 4) from each component value are grouped together, then our dot product reduces to a set of basic bitwise operations; AND + bit count for each component, followed by a shift representing the respective position of the query part, and lastly a sum to get the final result. See the BBQ blog for a more detailed explaination, but the following image visualizes an example query translation.
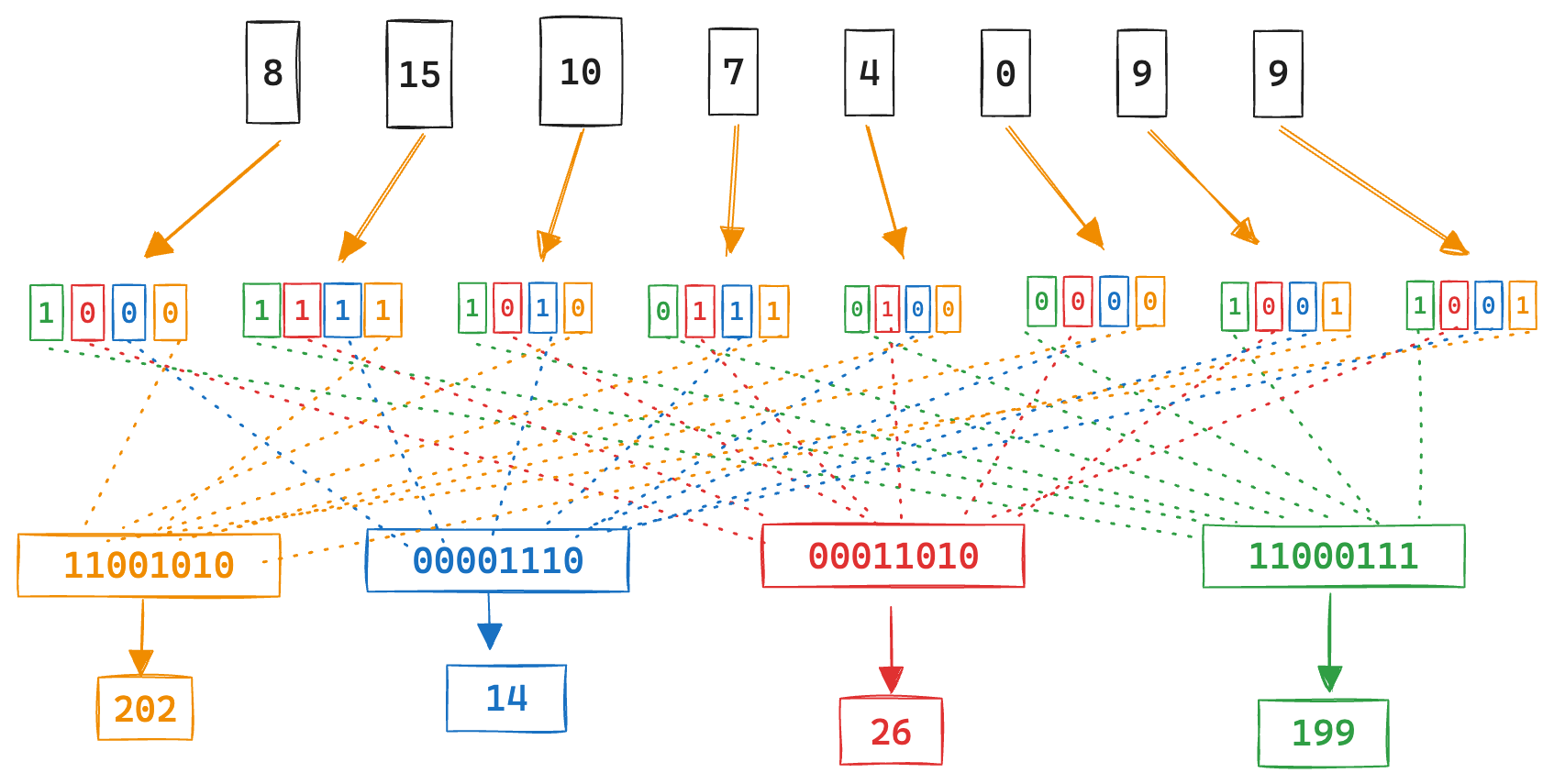
Logically, the dot product reduces to the following, where d is the stored vector, and q1, q2, q3, q4 are the respective positional parts of the translated query vector:
(bitCount(d & q1) << 0) + (bitCount(d & q2) << 1)
+ (bitCount(d & q3) << 2) + (bitCount(d & q4) << 3)For execution purposes, we layout the translated query parts, by increasing respective bit position, contiguously in memory. So we now have our translated query vector, q[], which is four times the size of that of the stored vector d[].
A scalar java implementation of this dot product looks like this:
byte[] d = ... // stored vector bits
byte[] q = ... // query bits
for (int i = 0; i < 4; i++) {
long subRet = 0;
for (int j = 0; j < d.length; j++) {
subRet += Integer.bitCount(q[i*d.length + j] & d[j] & 0xFF);
}
ret += subRet << i;
}While semantically correct, this implementation is not overly efficient. Let's move on and see what a more optimal implementation looks like, after which we can compare the runtime performance of each.
Where does the performance come from?
The implementation we've seen so far is a straightforward naive scalar implementation. To speed things up we rewrite the dot product with the Panama Vector API in order to explicitly target specific SIMD instructions.
Here's a simplified snippet of what the code looks like for just one of the query parts - remember we need to do this four times, one for each of the translated int4 query parts.
var sum = LongVector.zero(LongVector.SPECIES_256);
for (int i=0; i < BYTE_SPECIES_256.loopBound(d.length); i += BYTE_SPECIES_256.length()) {
var vq = ByteVector.fromArray(BYTE_SPECIES_256, q, i).reinterpretAsLongs();
var vd = ByteVector.fromArray(BYTE_SPECIES_256, d, i).reinterpretAsLongs();
sum = sum.add(vq.and(vd).lanewise(VectorOperators.BIT_COUNT));
}
long subRet = sum.reduceLanes(VectorOperators.ADD);
// tail processing, if any
ret += subRet << q_part // query part numberHere we're explicitly targeting AVX, operating on 256 bits per loop iteration. First performing a logical AND between the vq and vd, then a bit count on the result of that, before finally adding it to the sum accumulator. While we're interested in the bit count, we do however interpret the bytes in the vectors as longs, since that simplifies the addition and ensures that we don't risk overflowing the accumulator. A final step is then needed to horizontally reduce the lanes of the accumulator vector to a scalar result, before shifting by the representative query part number.
Disassembling this on my Intel Skylake, we can clearly see the body of the loop.
0x00007cf9bcd57430: movsxd r14,ecx
0x00007cf9bcd57433: vmovdqu ymm4,YMMWORD PTR [rsi+r14*1+0x10]
0x00007cf9bcd5743a: vmovdqu ymm5,YMMWORD PTR [rdx+r14*1+0x10]
0x00007cf9bcd57441: vpand ymm4,ymm4,ymm5
0x00007cf9bcd57445: vpopcntq ymm4,ymm4
0x00007cf9bcd5744b: vpaddq ymm3,ymm3,ymm4
0x00007cf9bcd5744f: add ecx,0x20
0x00007cf9bcd57452: cmp ecx,edi
0x00007cf9bcd57454: jl 0x00007cf9bcd57430
The rsi and rdx registers hold the address of the vectors to be compared, from which we load the next 256 bits into ymm4 and ymm5, respectively. With our values loaded we now perform a bitwise logical AND, vpand, storing the result in ymm4. Next you can see the population count instruction, vpopcntq, which counts the number of bits set to one. Finally we add 0x20 (32 x 8bits = 256bits) to the loop counter and continue.
We're not showing it here for simplicity, but we actually unroll the 4 query parts and perform them all per loop iteration, as this reduces the load of the data vector. We also use independent accumulators for each of the parts, before finally reducing.
There are 128 bit variants whenever the vector dimensions do not warrant striding 256 bits at a time, or on ARM where it compiles to sequences of Neon vector instructions AND, CNT, and UADDLP. And, of course, we deal with the tails in a scalar fashion, which thankfully doesn't occur all that often in practice given the dimension sizes that most popular models use. We continue our experiments with AVX 512, but so far it's not proven worthwhile to stride 512 bits at a time over this data layout, given common dimension sizes.
How much does SIMD improve things?
When we compare the scalar and vectorized dot product implementations, we see from 8x to 30x throughput improvement for a range of popular dimensions from 384 to 1536, respectively.
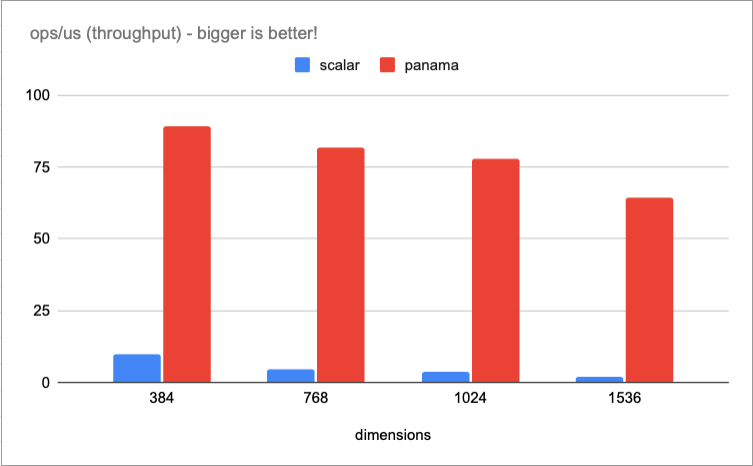
With the optimized dot product we have greatly improved the overall performance such that the vector comparison is no longer the single most dominant factor when searching and indexing with BBQ. For those interested, here are some links to the benchmarks and code.
Wrapping up
BBQ is a new technique that brings both incredible efficiencies and awesome performance. In this blog we looked at how vector distance comparison is optimized in BBQ by hardware accelerated SIMD instructions. You can read more about the index and search performance, along with accuracy and recall in the BBQ blog. BBQ is released as tech-preview in Elasticsearch 8.16, and in Serverless right now!
Along with new techniques like BBQ, we're continuously improving the low-level performance of our vector database. You can read more about what we've already done in these other blogs; FMA, FFM, and SIMD. Also, expect to see more of these low-level performance focused blogs like this one in the future, as we keep improving the performance of Elasticsearch so that it's the best place to store and search your vector data.
Ready to try this out on your own? Start a free trial.
Elasticsearch has integrations for tools from LangChain, Cohere and more. Join our advanced semantic search webinar to build your next GenAI app!
Related content

October 23, 2025
Low-memory benchmarking in DiskBBQ and HNSW BBQ
Benchmarking Elasticsearch latency, indexing speed, and memory usage for DiskBBQ and HNSW BBQ in low-memory environments.

October 22, 2025
Deploying a multilingual embedding model in Elasticsearch
Learn how to deploy an e5 multilingual embedding model for vector search and cross-lingual retrieval in Elasticsearch.

October 23, 2025
Introducing a new vector storage format: DiskBBQ
Introducing DiskBBQ, an alternative to HNSW, and exploring when and why to use it.
September 19, 2025
Using TwelveLabs’ Marengo video embedding model with Amazon Bedrock and Elasticsearch
Creating a small app to search video embeddings from TwelveLabs' Marengo model.

September 15, 2025
Balancing the scales: Making reciprocal rank fusion (RRF) smarter with weights
Exploring weighted reciprocal rank fusion (RRF) in Elasticsearch and how it works through practical examples.